Question #20: What does the cable equation mean for neurons?
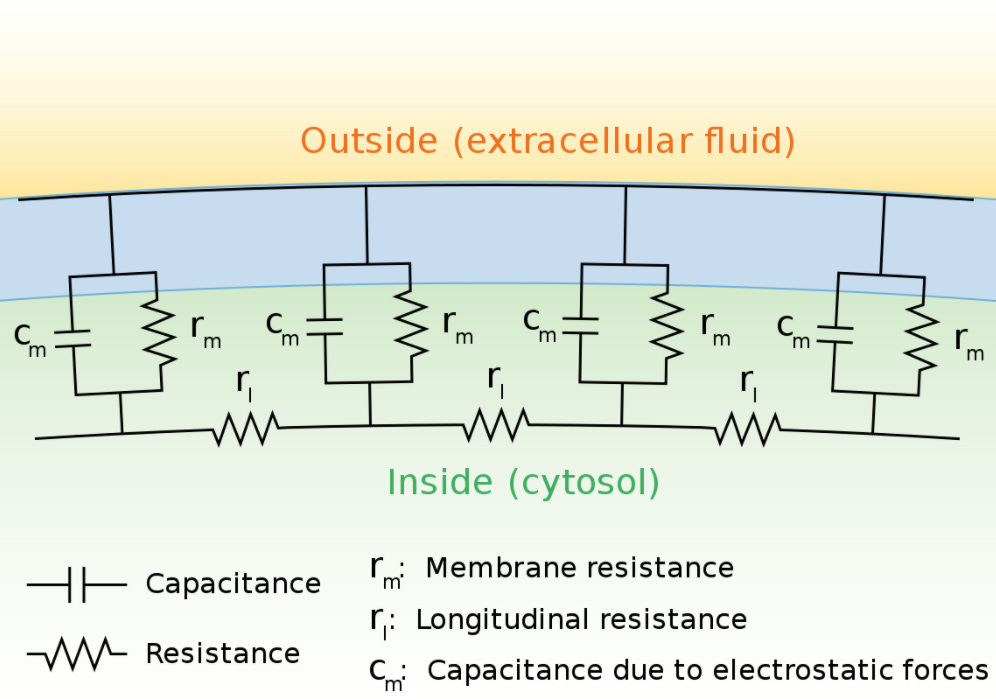
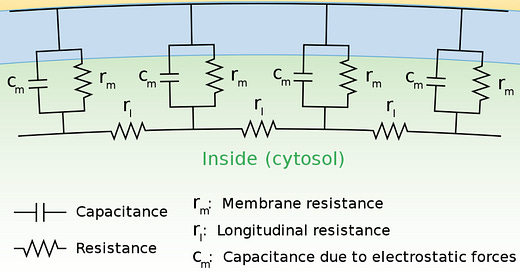
- Cable theory can be derived in part from Ohm's law, the fundamental theory of electricity that models the current flowing between two points as equal to the voltage distance between the two points divided by the material's resistance, or in other words, the classic equation V = IR.
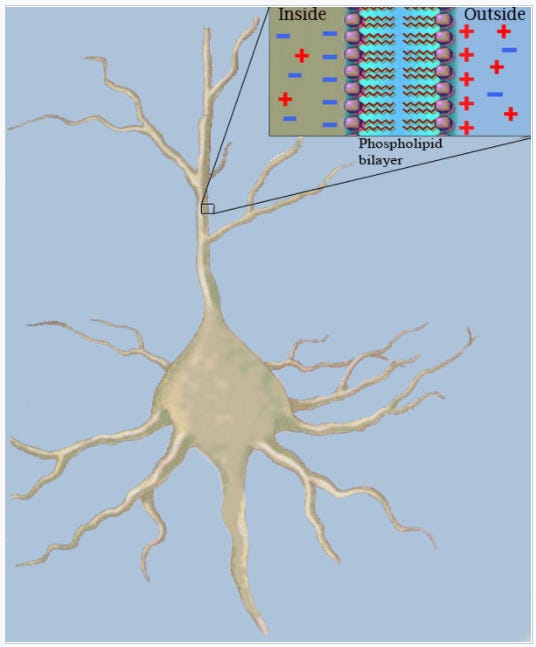
- The greater the cross-sectional area of the neurite's cytosol (the interior part of it, containing biomolecules, electrolytes, and other ions), the easier an ion can flow through it, so the neurite's longitudinal resistance, r_l, will be lower.
- If the cell membrane is more resistant to ion flow into or out of the cell (due to high membrane resistance, r_m), then charge will tend to accumulate inside the cell, and it will have a higher ionic current flowing down longer distances in the neurite. This is often represented by a paremeter called the length current, λ, equal to the square root of r_m divided by r_l.
- If a cell membrane has a lower membrane capacitance (c_m, which is usually a fairly constant value), then the relative ion flow down the neurite will be greater, due to a lower displacement current. How quickly the membrane voltage changes in response to a current injected at at given point can be predicted by the time constant, τ, equal to the product of c_m times r_m.
- An electrotonic potential results from a local change in ion conductance, e.g. after a synaptic event, that does not propagate. It becomes exponentially smaller as it spreads. This is opposed to an action potential, which reaches the voltage threshold by which it does propagate down the neurite (due to the opening of voltage-gated ion channels), and then spreads like a wave.
- Dendritic trees can perform non-linear integration of signals that can be predicted on the basis of cable theory. The existence of subthreshold membrane potential fluctuations in dendrites, which based on my understanding should dominate neuronal signaling, can allow variations in synaptic weight distributions and input timing to encode a substantial amount of information within a single neuron.
Inspired by CalTech’s Question #20 for cognitive scientists: “Derive the cable equation (for a uniform cylinder, with optimal boundary conditions). What does it mean for neurons?”